Summary on Goeree and Holt (2004)

Title: A model of noisy introspection Link to the paper.

Authors: Goeree, Holt

Year published: 2004

Journal: Games and Economic Behavior

This paper introduces "noisy introspection", a way of encoding randomness into higher-order belief formation, in order to better explain outcomes of a oneshot game

Outline

• In a oneshot game, players do not have time to learn about each other. They thus have to make their decisions based on silent speculation (introspection, I suppose).
• This introspecting is on what they believe the opponents are like/will do and what the opponents think they are like/will do and so on and so forth
• Thus higher order beliefs occur naturally in oneshot games because "they have to get it right on the first try"
• While it should be easy enough to find the Nash equilibrium in a \(2\times 2\) game, the outcome is quite different from the theoretical prediction (at least in the games that are analyzed by these two authors
• In particular, they revisited a number of oneshot game experiments reported by two psychologists (Guyer and Rapoport, 1972)
• One of the games looked like this

Row player's decision	Column player's decision
	S	R
S	10,19	4, -7
R	-14,4	19,10

• The Nash equilibrium is this

Row player's decision	Column player's decision
	S	R
S	10*,19*	4, -7
R	-14,4	19*,10*

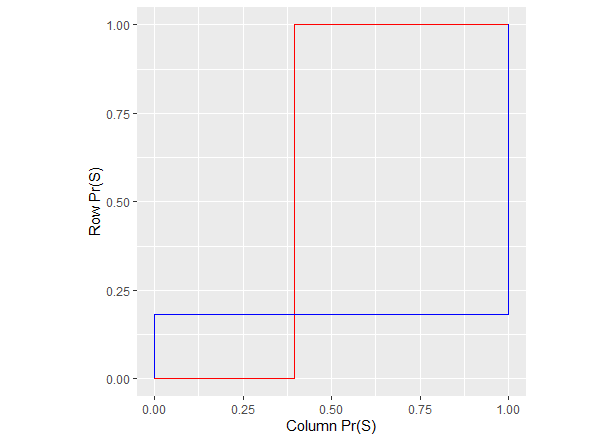
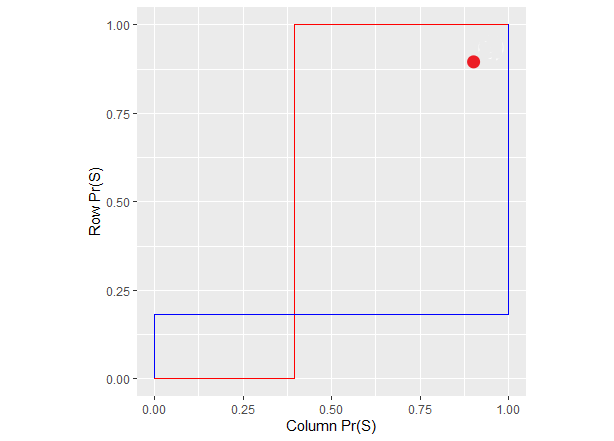
• Because there are two pure Nash equilibria there must also be at least one mixed equilibria, which is shown in this chart on the left. But the empirical findings were that the row and column players chose a point somewhere near (1,1), which is shown in the chart on the right.
• It turns out that one can introduce "random noise" into the decision-making process by calculating probabilities not with sharp jumps but with gentle jumps using a logit function based on the expected payoffs to player \(i\) \(\pi_{R,S}^i\) of choosing R or S, and some exogenous error term \(\mu\) $$p_i(S)=\frac{\exp(\pi_{i,S}^e/\mu)}{\exp(\pi_{i,S}^e/\mu)+\exp(\pi_{i,R}^e/\mu)} $$
• The use of this expression to find the probability of choosing S (or R) will lead to "softer" lines than the ones in the images above (I still need to figure out how exactly this is evaluated)
• But appaerently the higher \(\mu\) is, the lines only intersect once at a point that they call quantal response equilibrium